In this fourth and final essay of our series on the NumPy project we will combine two very important aspects of developing a (software) product: the technological aspect and the social aspect. As an architecture is designed, developed and built-upon by humans, the social side of the process should not be overlooked. Conway’s Law will play a central role in this techno-social analysis of the NumPy project.
We start out by explaining the relevance of the techno-social aspect of a project. Then, we continue by identifying loosely and tightly coupled components in the NumPy repository using information from previous essays and tools like Sigrid and CodeScene. After that, we will analyse the communication between the developers of NumPy using the GitHub GraphQL API Explorer and a custom-made Python script. We close off by assessing the results in relation to Conway’s Law.
NOTE: The formatting in this essay has been optimised for the online version.
- Techno-Social Congruence
- Component Coupling
- Developer Discussion
- Computing congruence and connection to Conway’s law
Techno-Social Congruence
You might think: ‘what even is Techno-Social Congruence and why does it matter?’. Well, Cataldo et al. propose the following:
We define socio-technical congruence as the match between the coordination requirements established by the dependencies among tasks and the actual coordination activities carried out by the engineers.1
This means that the congruence is determined by the technical dimension as well as the social dimension of a project. This is still a bit abstract, so let’s dive a bit deeper.
In software development, not only the engineering decisions have an impact on the result, organising the developers behind the project is also of importance. As argued by Conway there is a relation between the design of a system and the structure within the organisation behind it2. In the domain of software engineering, this can in general be seen as the software architecture relating to the structure in which the developers are organised.
When multiple developers are working on a project there is a chance that their code will interact or multiple developers are working on the same component. This is where techno-social congruence matters, if the communication between developers is improved, their output will likely also improve.
Cataldo et al. already propose a way to compute the congruence between the coordination that is needed while developing a component and the actual coordination happening between the developers1. The proposed method requires a large amount of data and manual analysis, so we decided to simply review the coupling between the different components and then compare this to the amount of communication between the developers while working on the components.
Component coupling
In this section we analyse the dependency relationships between the components that NumPy consists of. We do this by looking at the dependency graph provided by SIG through Sigrid. This graph shows the dependencies between components in terms of call relationships, inheritance relationships and C implement relationships3.
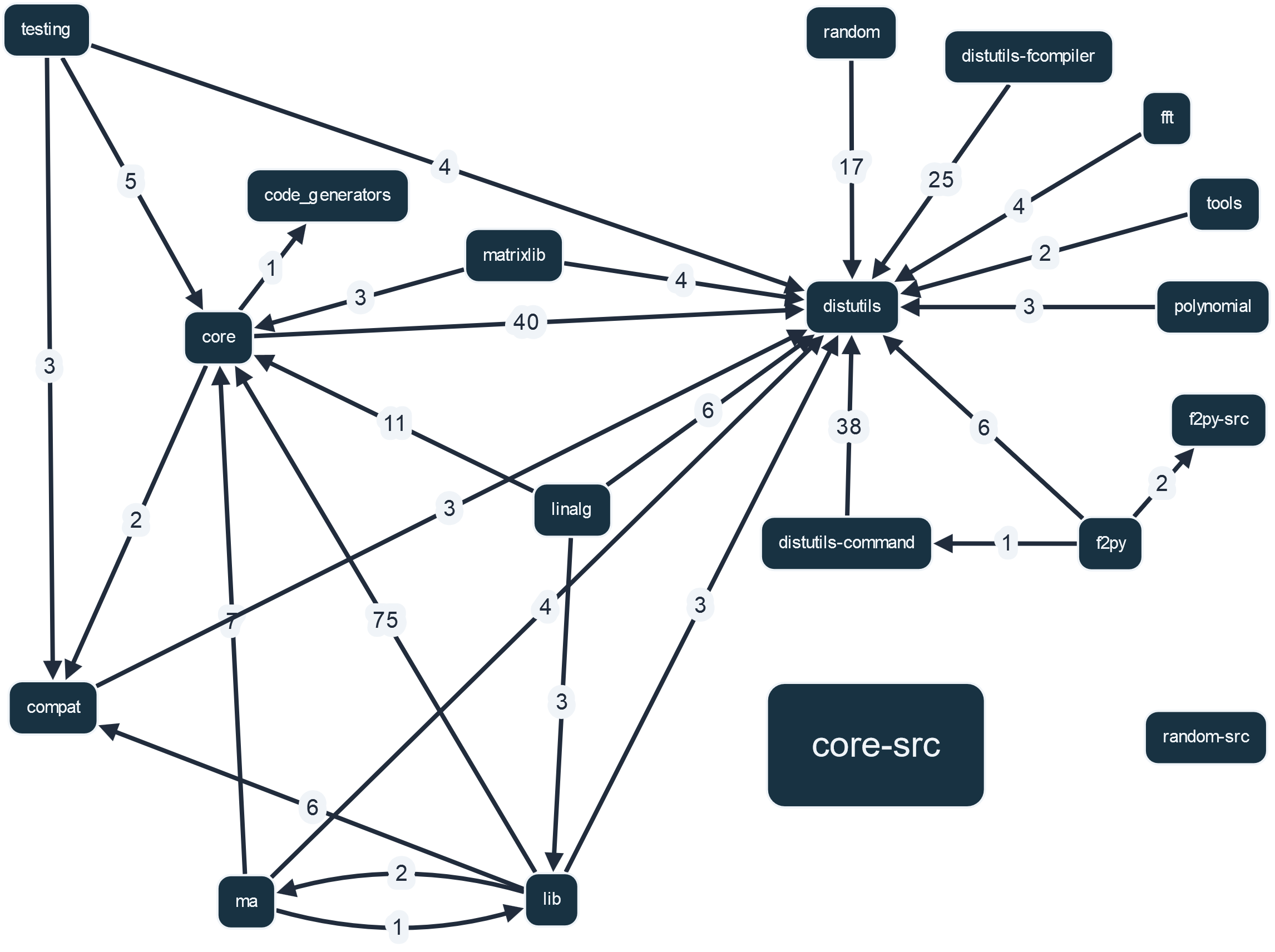
Figure: Dependency graph. Created by SIG.
One dependency that catches the eye is the dependency between the components lib and core. The core component contains the core of the NumPy functionality i.e. ndarray, ufuncs and dtypes. lib is mostly a space for implementing functions that don’t belong in core or in another NumPy submodule with a clear purpose such as fft, linalg or random. It is not a big surprise that lib depends so heavily on core because NumPy obviously stores a lot of functionality in the lib module.
Another striking feature of the image is that core-src and random-src are included as components, though do not appear to be coupled to other components. This is, of course,rather unlikely but can be explained by the way NumPy is set up and the origin of these components. For performance, NumPy’s core is written in C, as was elaborated upon in previous essays. The core-src and random-src components house this C-code. Communication from these components to the rest of NumPy’s codebase is done through core and random. Though core-src communicates with core, and random-src with random, it appears that Sigrid was not able to pick up this relationship between Python and C hybrid code when creating the dependency graph.
We kept the core-src and random-src components visible in this diagram to remain consistent with our previous component definitions. However, to interpret this diagram it is a good idea to regard core and core-src, and random and random-src as the same component.
Finally, the distutil module is called by all components. This is the case because distutils is a toolbox for distributing packages. Numpy provides extended distutil functionality to ease the process of building and installing sub-packages and auto-generating code Moreover, it provides extension modules that use Fortran-compiled libraries.
It is also worth noting that specific, library-like components such as linalg, random, fft, and polynomial have the same position in the project, being near-standalone libraries for specific mathematical functions. Therefore, it is to be expected that these components have no coupling between them.
Developer Discussion
The other side of Conway’s law is the communication between developers2. There are multiple commuincation channels for NumPy, there are the mailing lists4 and of course the GitHub repository itself. In the GitHub repository itself most communication happens in the issues and pull requests.
In order to analyse the communication patterns between developers we wrote a tool that counts the amount of comments of developers on GitHub. These comments are measured using the GitHub API. The tool itself is also open sourced on GitHub5.
The comments are counted per user and per component using labels. These labels specify the component the issue or pull request is about, for example: component: numpy.core. To calculate the overlap score of communication between 2 components for a certain user we use the following formula:
1 - ABS(#component A comments - #componentB comments)/(#component A comments + #component B comments)
This formula ranges from 0 to 1, when the amount of comments on both component A and B are similar the overlap score will be 1. If the amount of comments differs a lot the score will be closer to 0. We can take the average of these scores for the different users to get a total score for a component pair, which then also ranges from 0 to 1 but will likely be much lower as many users will have a score of 0. Here a high score would mean that users that comment in issues/PRs of component A also comment in issues/PRs of component B, which means that the users in this component pair communicate with eachother a lot.
Some noteworthy results for several component pairs are shown in the table below:
| core-lib | core-linalg | linalg-fft | linalg-polynomial | core-distutils | random-linalg | |
|---|---|---|---|---|---|---|
| Total score | 0,016687626 | 0,020836 | 0,009528 | 0,009761 | 0,012406203 | 0,016775517 |
As can be seen in the table the scores for linalg-fft and linalg-polynomial are significantly lower than the scores for core-lib and core-linalg. This brings us to the results of the analysis in the following section.
Computing congruence and connection to Conway’s law
Now that we have discussed the coupling between components and the discussion process of NumPy’s developers, we can compare these results and determine if Conway’s law appears to hold.
The analysis of dependencies between components told us that core and lib are tightly coupled and when we ran the github comment analysis tool we obtain a result that conways law predicted indeed. The output of the formula is 0,017163665 which is much higher than the output for linalg-fft for example, which was only 0,009279859.
Furthermore, it seems that communication between specific, library-like components such as linalg, fft, and polynomial is just as limited as the coupling measured in the coupling diagram from a few sections back (here). Namely, these components are not coupled at all, according to the diagram.
This seems to correspond to the scores measured in the previous section; 0,009528 for communication between linalg and fft, and 0,009761 for communication between linalg and polynomial. These scores are about 2 times lower than the score for core and lib.
However, the score for the relation random-linalg was 0,016775517 and this is remarklably high. We speculate that, even though it is reasonable to assume that linear algebra functions sometimes use random variables, such as for power iterations, random is a relatively separate library. This assumption is reflected in the graph as well.
We can see that in most cases Conway’s law seems to hold, there is namely more communication between more tightly coupled components and less communication in more loosely couple components. There are some cases in which Conway’s law matches the communication patterns less, but in general, we can conclude that the law applies to the NumPy project.
-
Cataldo, Herbsleb, and Carley. Socio-Technical Congruence: A Framework for Assessing the Impact of Technical and Work Dependencies on Software Development Productivity. ICSE 2008. https://herbsleb.org/web-pubs/pdfs/cataldo-socio-2008.pdf ↩ ↩2
-
Conway, M.E. 1968. How do committees invent? Datamation, 14, 5, 28-31. http://www.melconway.com/Home/Committees_Paper.html ↩ ↩2
-
Software Improvement Group user manual, retrieved 2020-03-26. https://sigrid-says.com/assets/sigrid_user_manual_20191224.pdf, ↩
-
NumPy mailing lists overview, retrieved 2020-04-08. https://www.scipy.org/scipylib/mailing-lists.html, ↩
-
GitHub Counter project page. https://github.com/Jimver/github-comment-counter, ↩